Este blog está dedicado a los múltiples sistemas electorales que hay o ha habido en el mundo, así como a los curiosos resultados que han producido, que pueden ir contra nuestra intuición o resultarnos curiosos.
Trato de explicar los diversos sistemas por comparación entre sí y sus posibles problemas mediante ejemplos reales, pero no me resisto a introducir de vez en cuando casos hipotéticos o explicaciones matemáticas, siempre con la intención de informar sin aburrir y sin someter al lector a esfuerzos inútiles.
Debo aclarar que es mi intención ser objetivo y dar la información sin mezclar mi opinión, sólo por el placer de divulgar. Sería más adecuado para este fin que el blog se titulara "Rarezas electorales", pero lo he llamado así por parecerme que llama más la atención y no se aleja mucho de la realidad, otro tema es si la trampa es fortuita o perseguida de forma consciente.
Sin más, os deseo que disfruteis tanto leyendo como yo escribiendo y no dudeis en comentar o incluso preguntar lo que os plazca.
lunes, 19 de marzo de 2012
domingo, 18 de marzo de 2012
Elecciones presidenciales en los Estados Unidos
Voy a empezar por los casos más simples y donde la rareza es más notoria, ¿puede haber algo más llamativo que una votación entre, básicamente, dos opciones y que pueda "ganar" la opción minoritaria?
Por eso he seleccionado éste sistema electoral como el primero a analizar, adelanto que la "trampa" se debe a la existencia de varios distritos (51) y se agrava al aplicar un sistema completamente "mayoritario". Paso a explicarlo:
USA se divide en distritos electorales o circunscripciones, que coinciden básicamente con los 50 estados, a los que les corresponde nombrar tantos delegados como congresistas tengan (que se adjudican a su vez de forma proporcional a la población del estado), y el Distrito de Columbia (la capital, que no tiene congresistas) a la que le corresponden 3 delegados (como al estado menos poblado). Cabe mencionar 2 curiosas excepciones, Nebraska y Maine, que se dividen a su vez en 3 y en 2 distritos respectivamente; al partido ganador en cada uno de estos le corresponde un delegado y al que gane en toda Nebraska le adjudican 2 delegados más, lo mismo en Maine. En el resto de distritos, el ganador en cada uno de ellos obtiene todos los delegados adjudicados al distrito.
Adjunto el mapa:
Después, los 538 delegados se reúnen para elegir Presidente y Vicepresidente de la República. Así, podría ocurrir que el partido más votado en toda la nación no lograra nada y el otro gran partido fuese quien gobernase, si obtuviere al menos 270 delegados. En el improbable caso de un empate a 269 el Congreso nombraría a ambos cargos, una de las cámaras al Presidente y la otra al Vicepresidente.
Imagínese, para entender mejor el supuesto, que un partido obtiene un voto más que el rival en estos estados:
California: 55
Texas: 34
Nueva York: 31
Florida: 27
Pensilvania: 21
Illinois: 21
Ohio: 20
Míchigan: 17
Nueva Jersey: 15
Carolina del Norte: 15
Georgia: 15
Con estos 11 votos más que el otro partido ya no importa no lograr ni un sólo voto en los demás estados, con lo que es posible perder por millones de votos y ser presidente.
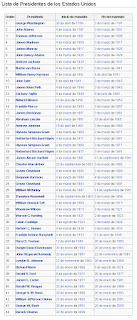
De hecho, más allá de la teoría, ha habido al menos 3 ocasiones en las que ha ocurrido precisamente eso: dos grandes partidos, uno gana en votos y otro en delegados. Ocurrió en 1876, 1888 y 2000. En los 3 casos el candidato demócrata ganó y gobernó el republicano. Aunque ha habido a lo largo de la historia más situaciones curiosas, por ello dejo una lista completa de las elecciones presidenciales de toda la historia estadounidense:
Dejo además los nombres y las fotos de los presidentes, por si a alguien le interesa.
En entradas sucesivas abundaré sobre el problema de los distritos.
Por eso he seleccionado éste sistema electoral como el primero a analizar, adelanto que la "trampa" se debe a la existencia de varios distritos (51) y se agrava al aplicar un sistema completamente "mayoritario". Paso a explicarlo:
USA se divide en distritos electorales o circunscripciones, que coinciden básicamente con los 50 estados, a los que les corresponde nombrar tantos delegados como congresistas tengan (que se adjudican a su vez de forma proporcional a la población del estado), y el Distrito de Columbia (la capital, que no tiene congresistas) a la que le corresponden 3 delegados (como al estado menos poblado). Cabe mencionar 2 curiosas excepciones, Nebraska y Maine, que se dividen a su vez en 3 y en 2 distritos respectivamente; al partido ganador en cada uno de estos le corresponde un delegado y al que gane en toda Nebraska le adjudican 2 delegados más, lo mismo en Maine. En el resto de distritos, el ganador en cada uno de ellos obtiene todos los delegados adjudicados al distrito.
Adjunto el mapa:
Después, los 538 delegados se reúnen para elegir Presidente y Vicepresidente de la República. Así, podría ocurrir que el partido más votado en toda la nación no lograra nada y el otro gran partido fuese quien gobernase, si obtuviere al menos 270 delegados. En el improbable caso de un empate a 269 el Congreso nombraría a ambos cargos, una de las cámaras al Presidente y la otra al Vicepresidente.
Imagínese, para entender mejor el supuesto, que un partido obtiene un voto más que el rival en estos estados:
California: 55
Texas: 34
Nueva York: 31
Florida: 27
Pensilvania: 21
Illinois: 21
Ohio: 20
Míchigan: 17
Nueva Jersey: 15
Carolina del Norte: 15
Georgia: 15
Con estos 11 votos más que el otro partido ya no importa no lograr ni un sólo voto en los demás estados, con lo que es posible perder por millones de votos y ser presidente.
De hecho, más allá de la teoría, ha habido al menos 3 ocasiones en las que ha ocurrido precisamente eso: dos grandes partidos, uno gana en votos y otro en delegados. Ocurrió en 1876, 1888 y 2000. En los 3 casos el candidato demócrata ganó y gobernó el republicano. Aunque ha habido a lo largo de la historia más situaciones curiosas, por ello dejo una lista completa de las elecciones presidenciales de toda la historia estadounidense:
Dejo además los nombres y las fotos de los presidentes, por si a alguien le interesa.
En entradas sucesivas abundaré sobre el problema de los distritos.
sábado, 17 de marzo de 2012
Sistema electoral del Reino Unido
En el Reino Unido solamente hay, a nivel nacional, elecciones a la Cámara de los Comunes; la otra cámara parlamentaria (la de los Lores) no es electa y tampoco hay elecciones presidenciales (es elegido por la Cámara de los Comunes) o de otro tipo, por ello me limitaré a analizar esas elecciones.
Toda la nación se divide en 650 circunscripciones, el número total de escaños, y se asignan al ganador en cada una de ellas. Puede imaginarse que la distorsión resultante en la proporción es similar a la que hemos visto en la cámara de delegados que elegía al presidente estadounidense, a pesar de que ahora cada distrito tiene un sólo escaño. Nuevamente podría ocurrir que un partido fuese el más votado en la mayoría de distritos, por un voto y no tuviese votos en los demás distritos; pero no hay nada más claro que un ejemplo real, las últimas elecciones (2015):
Podemos compararlo con un reparto equitativo en que cada escaño valga 46273 votos.
Partidos que deberían tener 25 escaños o incluso 83 se quedan a 1, un partido que debería tener más de 50 se queda a 8 y otro partido con menos votos obtiene 56 escaños. Y todo esto por no hablar de los casi 100 escaños extra que obtienen los conservadores. Una mayoría absoluta con el 36% de los votos (teniendo el segundo partido un 30%).
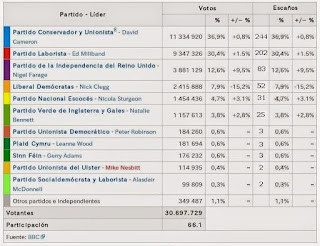
Y podemos ver también las penúltimas (2010):
Pongo también los gráficos, tanto el geográfico como el poblacional:
Pueden verse en la tabla cosas muy extrañas, como que el partido Alianza logre escaño con 42.000 votos y el partido por la independencia del Reino Unido no consiga nada con más de 900.000, o que la diferencia entre conservadores y laboristas sea de 50 escaños y 2 millones de votos, la misma diferencia se da entre laboristas y liberales, pero los últimos tienen 200 escaños menos que los primeros. Visto de otro modo, los liberales tienen más de la mitad de los votos que el partido vencedor y apenas la sexta parte de escaños.
Como no deseo extenderme más pondré la configuración de la cámara acorde a los votos (asignandole a cada escaño el mismo precio en votos):
Cada 44.508 votos se logra un escaño. De aquí se desprende que la dispersión del voto es penalizada (le ocurre al BNP y al UKIP que pierden todos sus 32 escaños) pero la excesiva concentración del voto también (una vez que ganas en un distrito no importa si has arrasado con un 90%, no te llevas más de 1 escaño, lo mismo que si ganas por un voto), por eso los nacionalistas escoceses sacan 6 escaños en vez de 11.
Casos más raros se han dado en el pasado:
Como puede verse, se han producido gobiernos de candidatos perdedores, como en USA. He añadido tambien las elecciones de 1895 porque el primer partido, con 100.000 votos más, obtiene más del doble de los escaños del segundo y el tercer partido, con 11 veces menos votos que el segundo, llega a obtener la mitad de sus escaños. Lo que significa que el sistema no favorece a los partidos más grandes ni a los más pequeños (en esta ocasión el primero y el tercero se benefician y el segundo es el gran perjudicado). En este país, a diferencia del anterior, la cámara no se disuelve al elegir jefe de gobierno, sino que legisla durante 5 años, por lo que la desproporción hará que se aprueben o rechacen leyes con un criterio distinto al del pueblo.
Pero hay algo aún más curioso, la desproporción que generan las circunscripciones múltiples puede no ser fortuita sino manejada conscientemente, si los distritos no están fijos (en el Reino Unido el gobierno los modifica de una elección a otra, con la única condición de que contengan el mismo número de personas cada uno y su territorio sea continuo).
Toda la nación se divide en 650 circunscripciones, el número total de escaños, y se asignan al ganador en cada una de ellas. Puede imaginarse que la distorsión resultante en la proporción es similar a la que hemos visto en la cámara de delegados que elegía al presidente estadounidense, a pesar de que ahora cada distrito tiene un sólo escaño. Nuevamente podría ocurrir que un partido fuese el más votado en la mayoría de distritos, por un voto y no tuviese votos en los demás distritos; pero no hay nada más claro que un ejemplo real, las últimas elecciones (2015):
Podemos compararlo con un reparto equitativo en que cada escaño valga 46273 votos.
Partidos que deberían tener 25 escaños o incluso 83 se quedan a 1, un partido que debería tener más de 50 se queda a 8 y otro partido con menos votos obtiene 56 escaños. Y todo esto por no hablar de los casi 100 escaños extra que obtienen los conservadores. Una mayoría absoluta con el 36% de los votos (teniendo el segundo partido un 30%).
Y podemos ver también las penúltimas (2010):
Como no deseo extenderme más pondré la configuración de la cámara acorde a los votos (asignandole a cada escaño el mismo precio en votos):
Cada 44.508 votos se logra un escaño. De aquí se desprende que la dispersión del voto es penalizada (le ocurre al BNP y al UKIP que pierden todos sus 32 escaños) pero la excesiva concentración del voto también (una vez que ganas en un distrito no importa si has arrasado con un 90%, no te llevas más de 1 escaño, lo mismo que si ganas por un voto), por eso los nacionalistas escoceses sacan 6 escaños en vez de 11.
Casos más raros se han dado en el pasado:
Como puede verse, se han producido gobiernos de candidatos perdedores, como en USA. He añadido tambien las elecciones de 1895 porque el primer partido, con 100.000 votos más, obtiene más del doble de los escaños del segundo y el tercer partido, con 11 veces menos votos que el segundo, llega a obtener la mitad de sus escaños. Lo que significa que el sistema no favorece a los partidos más grandes ni a los más pequeños (en esta ocasión el primero y el tercero se benefician y el segundo es el gran perjudicado). En este país, a diferencia del anterior, la cámara no se disuelve al elegir jefe de gobierno, sino que legisla durante 5 años, por lo que la desproporción hará que se aprueben o rechacen leyes con un criterio distinto al del pueblo.
Pero hay algo aún más curioso, la desproporción que generan las circunscripciones múltiples puede no ser fortuita sino manejada conscientemente, si los distritos no están fijos (en el Reino Unido el gobierno los modifica de una elección a otra, con la única condición de que contengan el mismo número de personas cada uno y su territorio sea continuo).
viernes, 16 de marzo de 2012
Gerrymandering
Como ya dije en la entrada anterior, la existencia de muchos distritos electorales crea desproporciones, que pueden ser manipuladas consciente y cuidadosamente por parte de la autoridad del momento, para lograr el mejor resultado posible con los votos que hay. A esta práctica se le llama Gerrymandering.
El curioso nombre se debe al gobernador de Massachusetts en 1812, Elbridge Gerry, quien unificó los distritos del Norte y Oeste del estado (en que su partido siempre perdía) para reducir la representación del otro gran partido. La forma que adoptó el nuevo distrito era el de una salamandra (salamander en inglés), y a esa práctica se la llamó desde entonces Gerrymandering (hacer salamandras de Gerry).
La trampa consiste basicamente en que gane la oposición por mucho en pocos distritos y que tu partido gane por poco en muchos distritos, así se economizan tus votos y se desperdician los del rival.
Un claro ejemplo de esta práctica es la creación del distrito 4º de Illinois o el 6º de Pennsilvania:
En efecto, en las elecciones a la Cámara de Representantes de los Estados Unidos se utiliza un sistema similar al del Reino Unido, a cada estado le corresponden unos escaños proporcionales a su población y estos se adjudican dividiendo el estado en distritos de 1 diputado.
Otro ejemplo de esta práctica la encontramos en Venezuela, en las elecciones legislativas, donde tambien se dividen los estados en distritos de 1 diputado. Estos son los resultados oficiales de 2010:
Debo aclarar que en cada estado se eligen además 2 diputados de forma proporcional, pero que no reducen la desproporción porque van 1 para cada partido (salvo que un partido saque más del doble de votos que el siguiente partido) y sólo engordan el parlamento. En Zulia, Miranda, Carabobo y la capital se eligen 3 en vez de 2 (2 para el ganador, 1 para el segundo), que modifica poco la composición del parlamento.
Los resultados mas impactantes son los de Carabobo, Mérida y la capital. A nivel nacional PSUV tiene 98 escaños con 48,13% de los votos y MUD 65 con 47,22%, una diferencia de apenas 100.000 votos.
Es fácil imaginar lo importante que resulta el diseño del mapa electoral, pondré un último ejemplo, ficticio:
Si le toca dividir el estado en 4 distritos al partido negro lo hará así y se llevara 3 escaños:
Si le toca al partido blanco lo hará de este modo y se llevará 3 escaños:
Los votos son los mismos, pero arrojan resultados distintos, dando ganador a uno u otro partido. Los cuadrados representan a 36 personas que eligen entre el partido blanco o el negro para repartir 4 escaños.
El curioso nombre se debe al gobernador de Massachusetts en 1812, Elbridge Gerry, quien unificó los distritos del Norte y Oeste del estado (en que su partido siempre perdía) para reducir la representación del otro gran partido. La forma que adoptó el nuevo distrito era el de una salamandra (salamander en inglés), y a esa práctica se la llamó desde entonces Gerrymandering (hacer salamandras de Gerry).
La trampa consiste basicamente en que gane la oposición por mucho en pocos distritos y que tu partido gane por poco en muchos distritos, así se economizan tus votos y se desperdician los del rival.
Un claro ejemplo de esta práctica es la creación del distrito 4º de Illinois o el 6º de Pennsilvania:
En efecto, en las elecciones a la Cámara de Representantes de los Estados Unidos se utiliza un sistema similar al del Reino Unido, a cada estado le corresponden unos escaños proporcionales a su población y estos se adjudican dividiendo el estado en distritos de 1 diputado.
Otro ejemplo de esta práctica la encontramos en Venezuela, en las elecciones legislativas, donde tambien se dividen los estados en distritos de 1 diputado. Estos son los resultados oficiales de 2010:
Los resultados mas impactantes son los de Carabobo, Mérida y la capital. A nivel nacional PSUV tiene 98 escaños con 48,13% de los votos y MUD 65 con 47,22%, una diferencia de apenas 100.000 votos.
Es fácil imaginar lo importante que resulta el diseño del mapa electoral, pondré un último ejemplo, ficticio:
Los votos son los mismos, pero arrojan resultados distintos, dando ganador a uno u otro partido. Los cuadrados representan a 36 personas que eligen entre el partido blanco o el negro para repartir 4 escaños.
jueves, 15 de marzo de 2012
Modificación de escaños
Visto lo anterior cabría pensar que el problema radica en el sistema mayoritario, en el que se le da todo al ganador de cada distrito (sea un escaño o varios), y que el problema se resolvería si hubiera un puñado de escaños por distrito y el reparto de los mismos fuera proporcional a los votos. Resulta que no es así, efectivamente el sistema mayoritario amplía la desproporción, pero no es el único causante.
Para explicar bien esto pondré un ejemplo real, las elecciones de Castilla-La Mancha en 2011. Se reparten los escaños entre sus cinco provincias (Guadalajara, Toledo, Cuenca, Ciudad Real y Albacete), después se asignan los escaños de cada una de las provincias a los partidos que se han presentado en ellas, de forma proporcional a los votos. Puede ocurrir (y ocurre) que un partido gane en una provincia y pierda en las otras cuatro, que pierda globalmente. Si la diferencia en cada provincia, entre los dos grandes partidos, fuera pequeña y la única provincia en la que ha ganado un partido fuera la que tiene un numero impar de escaños, ese partido tendría más escaños aunque tuviera menos votos.
Esto mismo es lo que intentó el presidente Jose María Barreda al cambiar de 47 a 49 el número de escaños totales, las provincias que recibían los nuevos escaños eran Toledo (que pasaba a tener una cantidad par de escaños) y Ciudad Real (que pasaba a tener número impar). Ciudad Real es la única provincia en la que ganó el PSOE, pero ocurrió que en Guadalajara el PP sacó tanta ventaja que se llevo 5 de los 8 diputados asignados: GAME OVER
Si en Guadalajara 5.241 personas hubieran votado PSOE en vez de PP el resultado habría sido:
PP 58.878
PSOE 54.192
(4 escaños para cada uno)
Y en total:
PP 559.094
PSOE 513.957
Victoria en votos para el PP (con solo 24 diputados) y derrota para el PSOE (con 25 diputados que le dan mayoría absoluta).
Lo que demuestra que es posible caer en el mismo problema comentado en entradas anteriores al haber varias circunscripciones electorales. Aquí no se trata de modificar los distritos o sobrerrepresentar un territorio, basta con variar el número de escaños del Parlamento.
Algo parecido tenía en mente el presidente andaluz Jose Antonio Griñán, pero a lo bestia, planeaba subir el número de escaños del parlamento de 109 (ha permanecido así desde que se creó el Parlamento andaluz en 1982) a 135, para que los escaños se repartan también entre UPyD y PA; no sólo entre IU, PSOE y PP, de ese modo aunque el PP ganase no obtendría mayoría absoluta, pero ha acabado desechando esta idea al conocer la decisión de UPyD de no garantizar un pacto con PSOE y la de PA de negociar con PP.
Explicaré más adelante la forma en que se asignan escaños a cada circunscripción y el funcionamiento de los sistemas "proporcionales", temas que hasta ahora he nombrado de pasada.
Para explicar bien esto pondré un ejemplo real, las elecciones de Castilla-La Mancha en 2011. Se reparten los escaños entre sus cinco provincias (Guadalajara, Toledo, Cuenca, Ciudad Real y Albacete), después se asignan los escaños de cada una de las provincias a los partidos que se han presentado en ellas, de forma proporcional a los votos. Puede ocurrir (y ocurre) que un partido gane en una provincia y pierda en las otras cuatro, que pierda globalmente. Si la diferencia en cada provincia, entre los dos grandes partidos, fuera pequeña y la única provincia en la que ha ganado un partido fuera la que tiene un numero impar de escaños, ese partido tendría más escaños aunque tuviera menos votos.
Esto mismo es lo que intentó el presidente Jose María Barreda al cambiar de 47 a 49 el número de escaños totales, las provincias que recibían los nuevos escaños eran Toledo (que pasaba a tener una cantidad par de escaños) y Ciudad Real (que pasaba a tener número impar). Ciudad Real es la única provincia en la que ganó el PSOE, pero ocurrió que en Guadalajara el PP sacó tanta ventaja que se llevo 5 de los 8 diputados asignados: GAME OVER
Si en Guadalajara 5.241 personas hubieran votado PSOE en vez de PP el resultado habría sido:
PP 58.878
PSOE 54.192
(4 escaños para cada uno)
Y en total:
PP 559.094
PSOE 513.957
Victoria en votos para el PP (con solo 24 diputados) y derrota para el PSOE (con 25 diputados que le dan mayoría absoluta).
Lo que demuestra que es posible caer en el mismo problema comentado en entradas anteriores al haber varias circunscripciones electorales. Aquí no se trata de modificar los distritos o sobrerrepresentar un territorio, basta con variar el número de escaños del Parlamento.
Algo parecido tenía en mente el presidente andaluz Jose Antonio Griñán, pero a lo bestia, planeaba subir el número de escaños del parlamento de 109 (ha permanecido así desde que se creó el Parlamento andaluz en 1982) a 135, para que los escaños se repartan también entre UPyD y PA; no sólo entre IU, PSOE y PP, de ese modo aunque el PP ganase no obtendría mayoría absoluta, pero ha acabado desechando esta idea al conocer la decisión de UPyD de no garantizar un pacto con PSOE y la de PA de negociar con PP.
Explicaré más adelante la forma en que se asignan escaños a cada circunscripción y el funcionamiento de los sistemas "proporcionales", temas que hasta ahora he nombrado de pasada.
miércoles, 14 de marzo de 2012
La paradoja de Alabama
Para asignar a cada circunscripción o distrito electoral los escaños que le corresponden del total se suele usar un sistema "del resto mayor". En el congreso de España se utiliza el método Hare o regla de Hamilton.
El número de escaños de una provincia debe estar en la misma proporción con los escaños totales, que la población de ésta respecto de la población total de la nación, si despejamos esa regla de 3 podríamos decir que "q = pn/m" donde 'p' es la población de la circunscripción, 'm' la población total de la nación, 'q' los escaños del distrito y 'n' el número de escaños totales.
Como el número 'q' de escaños de cada distrito no suele salir entero, hay que aproximarlo hacia abajo. Hecho esto sobrará algún escaño sin asignar a ningún distrito que se le asignará finalmente a los distritos que tienen la parte decimal más grande.
Un ejemplo para comprender esto es el reparto de escaños en las elecciones generales españolas de 2008 entre todas las provincias, aunque debo advertir que inicialmente Ceuta y Melilla cuentan con 1 escaño cada una y cada provincia con 2, los 248 restantes se reparten así:
m = 45.200.737
n = 248
n/m = 1/182.261
Los 26 escaños restantes son para las 26 provincias resaltadas en amarillo (las de mayor parte decimal).
Este método se usaba en Estados Unidos para asignar escaños a los estados federados en 1880, cuando surgió una curiosa situación: para modificar el número de escaños de la cámara con vistas a futuras elecciones, se hizo un estudio de repartos con una cámara de diferentes tamaños desde 270 a 350 miembros.
Entonces se observó que Alabama tenía derecho a 8 representantes si el tamaño de la cámara era de 299, pero disminuía a 7 representantes si el tamaño de la cámara era de 300.
El congreso decidió entonces adoptar un tamaño de 325 escaños, ya que ese número no parecía presentar problemas.
Este hecho se conoce con el nombre de paradoja de Alabama y se dice que el método de Hare no es monótono, ya que si se aumenta el número de escaños a repartir, con las mismos datos de población, sorprendentemente puede que haya estados que disminuyan su número de representantes.
Existen variantes de este sistema de reparto, como el método Droop o Imperiali, en el que se utilizan las fórmulas "q = p(n+1)/(m+n+1)" y "q = p(n+2)/m" respectivamente. A todos estos sistemas se les conoce como "del resto mayor" por la forma en que se asignan los escaños sobrantes.
Todos estos sistemas tienen el mismo problema, la paradoja de la población, que es similar a la de Alabama:
Si se mantienen fijos el número de circunscripciones y escaños del Parlamento pero varía la población, entonces un estado puede perder un representante en favor de otro, incluso si la población del primero crece y la del segundo disminuye. Veamos esto con un ejemplo:
Supongamos que tenemos una cámara de 6 escaños a repartir entre 4 provincias que llamaremos A, B, C y D y usaremos el método Hare.
Años después la población varía:
La provincia D está ahora más poblada y A y B han perdido habitantes, sin embargo D pierde un escaño en favor de A.
Ahora pondré un ejemplo de la paradoja de Alabama, también con Hare:
Tenemos 3 partidos (A, B y C) con 940.000, 9.030.000 y 10.030.000 votos respectivamente, observemos la diferencia entre repartir 200 escaños o 201.
El partido A pierde un escaño (pasa de 10 a 9) al repartirse un escaño más (de 200 a 201).
Debo añadir a estas dos la paradoja de las alternativas irrelevantes, que ha descubierto Alejandro Hurtado, uno de los seguidores de este blog.
Vamos a repartir 20 escaños entre 3 partidos:
Ahora añadiremos 4 partidos más, con pocos votos y que no se llevarán ningún escaño, pero aún así modificarán el reparto de escaños de los demás partidos al aumentar el total de votos de 961 a 1000.
El método Hare puede sufrir la paradoja de Alabama y además, como todos los sistemas "del resto mayor", la paradoja de la población y la paradoja de las alternativas irrelevantes. A pesar de eso, estos sistemas no sólo se utilizan para asignar escaños a las circunscripciones electorales, sino también (en algunos países) para asignar dentro de ellas escaños a los partidos en relación a sus votos.
El número de escaños de una provincia debe estar en la misma proporción con los escaños totales, que la población de ésta respecto de la población total de la nación, si despejamos esa regla de 3 podríamos decir que "q = pn/m" donde 'p' es la población de la circunscripción, 'm' la población total de la nación, 'q' los escaños del distrito y 'n' el número de escaños totales.
Como el número 'q' de escaños de cada distrito no suele salir entero, hay que aproximarlo hacia abajo. Hecho esto sobrará algún escaño sin asignar a ningún distrito que se le asignará finalmente a los distritos que tienen la parte decimal más grande.
Un ejemplo para comprender esto es el reparto de escaños en las elecciones generales españolas de 2008 entre todas las provincias, aunque debo advertir que inicialmente Ceuta y Melilla cuentan con 1 escaño cada una y cada provincia con 2, los 248 restantes se reparten así:
m = 45.200.737
n = 248
n/m = 1/182.261
Entonces se observó que Alabama tenía derecho a 8 representantes si el tamaño de la cámara era de 299, pero disminuía a 7 representantes si el tamaño de la cámara era de 300.
El congreso decidió entonces adoptar un tamaño de 325 escaños, ya que ese número no parecía presentar problemas.
Este hecho se conoce con el nombre de paradoja de Alabama y se dice que el método de Hare no es monótono, ya que si se aumenta el número de escaños a repartir, con las mismos datos de población, sorprendentemente puede que haya estados que disminuyan su número de representantes.
Existen variantes de este sistema de reparto, como el método Droop o Imperiali, en el que se utilizan las fórmulas "q = p(n+1)/(m+n+1)" y "q = p(n+2)/m" respectivamente. A todos estos sistemas se les conoce como "del resto mayor" por la forma en que se asignan los escaños sobrantes.
Todos estos sistemas tienen el mismo problema, la paradoja de la población, que es similar a la de Alabama:
Si se mantienen fijos el número de circunscripciones y escaños del Parlamento pero varía la población, entonces un estado puede perder un representante en favor de otro, incluso si la población del primero crece y la del segundo disminuye. Veamos esto con un ejemplo:
Supongamos que tenemos una cámara de 6 escaños a repartir entre 4 provincias que llamaremos A, B, C y D y usaremos el método Hare.
| Hare | A | B | C | D |
| Población | 208560 | 82000 | 38000 | 30000 |
| Cuota | 3.49 | 1.37 | 0.64 | 0.50 |
| Escaños | 3 | 1 | 0+1 | 0+1 |
Años después la población varía:
| Hare | A | B | C | D |
| Población | 206600 | 72000 | 38000 | 32000 |
| Cuota | 3.56 | 1.24 | 0.65 | 0.55 |
| Escaños | 3+1 | 1 | 0+1 | 0 |
La provincia D está ahora más poblada y A y B han perdido habitantes, sin embargo D pierde un escaño en favor de A.
Ahora pondré un ejemplo de la paradoja de Alabama, también con Hare:
Tenemos 3 partidos (A, B y C) con 940.000, 9.030.000 y 10.030.000 votos respectivamente, observemos la diferencia entre repartir 200 escaños o 201.
| Hare | A | B | C |
| Votos | 940.000 | 9.030.000 | 10.030.000 |
| Cuota | 9,4 | 90,3 | 100,3 |
| Escaños | 9+1 | 90 | 100 |
| Hare | A | B | C |
| Votos | 940.000 | 9.030.000 | 10.030.000 |
| Cuota | 9,447 | 90,7515 | 100,8015 |
| Escaños | 9 | 90+1 | 100+1 |
El partido A pierde un escaño (pasa de 10 a 9) al repartirse un escaño más (de 200 a 201).
Debo añadir a estas dos la paradoja de las alternativas irrelevantes, que ha descubierto Alejandro Hurtado, uno de los seguidores de este blog.
Vamos a repartir 20 escaños entre 3 partidos:
| Hare | A | B | C |
| Votos | 800 | 150 | 11 |
| Cuota | 16.65 | 3.12 | 0.23 |
| Escaños | 16+1 | 3 | 0 |
Ahora añadiremos 4 partidos más, con pocos votos y que no se llevarán ningún escaño, pero aún así modificarán el reparto de escaños de los demás partidos al aumentar el total de votos de 961 a 1000.
| Hare | A | B | C | D | E | F | G |
| Votos | 800 | 150 | 11 | 10 | 10 | 10 | 9 |
| Cuota | 16 | 3 | 0.22 | 0.20 | 0.20 | 0.20 | 0.18 |
| Escaños | 16 | 3 | 0+1 | 0 | 0 | 0 | 0 |
El método Hare puede sufrir la paradoja de Alabama y además, como todos los sistemas "del resto mayor", la paradoja de la población y la paradoja de las alternativas irrelevantes. A pesar de eso, estos sistemas no sólo se utilizan para asignar escaños a las circunscripciones electorales, sino también (en algunos países) para asignar dentro de ellas escaños a los partidos en relación a sus votos.
martes, 13 de marzo de 2012
La operación "Avispa"
Como hemos visto hasta ahora, los sistemas electorales "del residuo" o de "restos mayores" tienen grandes problemas y es posible que un partido se aproveche de ellos para obtener más escaños.
En Colombia el Partido Liberal puso en práctica, con mucho éxito, la operación "Avispa"; consistente en presentar muchas listas a las elecciones con la intención de obtener votos de "los restos". Efectivamente logró aumentar su representación muy por encima de lo que proporcionalmente le correspondía. En las elecciones legislativas de 2002, de los 100 escaños al senado por la circunscripción general, menos de 10 escaños fueron elegidos por cociente, un escaño fue elegido por residuo de una lista que obtuvo algún otro por cociente y los restantes escaños fueron elegidos por residuo.
Para entender mejor esto recordaré que cada lista sólo puede obtener de los restos un escaño, pero varias listas pueden obtener varios escaños. En el caso de 2 listas para repartir 2 escaños, si la lista minoritaria recibe el 26% de los votos garantiza un puesto, aunque la lista mayoritaria supere a la minoritaria en casi tres veces. El partido mayoritario, con 74%, obtiene un puesto por cociente del 50% (100/2), y le queda un residuo de 24%, inferior al residuo del 26% de la lista minoritaria. En cambio, asignando a cada escaño el mismo valor en votos (por ejemplo 1 escaño por cada 37% de los votos) se quedaría el partido mayoritario con ambos.
Lo ilustraré ahora con un ejemplo más completo. Utilizando el método Hare, se presentan cuatro partidos, el Partido A presenta tres listas, el partido B dos listas, y los partidos C, D, E y F una lista cada uno. Para elegir 10 escaños, las listas reciben los siguientes votos:
Esto otorga 4 escaños al partido A (33.500 votos), 2 al partido B (21.300 votos), 3 al partido C (34.300 votos) y 1 al partido D (4.900 votos). Los partidos E (4.200 votos) y F (1.800 votos) no obtienen escaños. Así, el partido A recibe menos votos que el partido C pero consigue más escaños.
Si los partidos A y B se hubieran presentado con listas únicas, el reparto de escaños habría variado:
El partido A tendría un escaño menos, el cual gana el partido C.
En la práctica es imposible prohibir a un partido dividirse en varios y aunque este sistema inicialmente sobrerrepresenta a los partidos pequeños y perjudica a los grandes, los partidos grandes pueden dividirse en partidos pequeños cuando lo deseen (y de un partido grande salen muchos pequeños, por lo que tendrán ventaja enfrentandose a una cantidad menor de partidos del mismo tamaño) obteniendo una gran ventaja, mayor que si se hubiera utilizado un sistema más equitativo.
En Colombia el Partido Liberal puso en práctica, con mucho éxito, la operación "Avispa"; consistente en presentar muchas listas a las elecciones con la intención de obtener votos de "los restos". Efectivamente logró aumentar su representación muy por encima de lo que proporcionalmente le correspondía. En las elecciones legislativas de 2002, de los 100 escaños al senado por la circunscripción general, menos de 10 escaños fueron elegidos por cociente, un escaño fue elegido por residuo de una lista que obtuvo algún otro por cociente y los restantes escaños fueron elegidos por residuo.
Para entender mejor esto recordaré que cada lista sólo puede obtener de los restos un escaño, pero varias listas pueden obtener varios escaños. En el caso de 2 listas para repartir 2 escaños, si la lista minoritaria recibe el 26% de los votos garantiza un puesto, aunque la lista mayoritaria supere a la minoritaria en casi tres veces. El partido mayoritario, con 74%, obtiene un puesto por cociente del 50% (100/2), y le queda un residuo de 24%, inferior al residuo del 26% de la lista minoritaria. En cambio, asignando a cada escaño el mismo valor en votos (por ejemplo 1 escaño por cada 37% de los votos) se quedaría el partido mayoritario con ambos.
Lo ilustraré ahora con un ejemplo más completo. Utilizando el método Hare, se presentan cuatro partidos, el Partido A presenta tres listas, el partido B dos listas, y los partidos C, D, E y F una lista cada uno. Para elegir 10 escaños, las listas reciben los siguientes votos:
| Partidos: | Partido A | Partido B | Partido C (lista única) | Partido D (lista única) | Partido E (lista única) | Partido F (lista única) | TOTAL | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Listas: | Lista 1 | Lista 2 | Lista 3 | Lista 4 | Lista 5 | ||||||
| votos: | 18.000 | 7.000 | 8.500 | 19.000 | 2.300 | 34.300 | 4.900 | 4.200 | 1.800 | 100.000 | |
| cociente: | 10.000 | ||||||||||
| escaños por cociente: | 1 | 0 | 0 | 1 | 0 | 3 | 0 | 0 | 0 | 5 | |
| votos por cociente: | 10.000 | 0 | 0 | 10.000 | 0 | 30.000 | 0 | 0 | 0 | 50.000 | |
| votos de residuo: | 8.000 | 7.000 | 8.500 | 9.000 | 2.300 | 4.300 | 4.900 | 4.200 | 1.800 | 50.000 | |
| escaños por residuo: | +1 | +1 | +1 | +1 | 0 | 0 | +1 | 0 | 0 | 5 | |
| Total de escaños: | 2 | 1 | 1 | 2 | 0 | 3 | 1 | 0 | 0 | 10 | |
Esto otorga 4 escaños al partido A (33.500 votos), 2 al partido B (21.300 votos), 3 al partido C (34.300 votos) y 1 al partido D (4.900 votos). Los partidos E (4.200 votos) y F (1.800 votos) no obtienen escaños. Así, el partido A recibe menos votos que el partido C pero consigue más escaños.
Si los partidos A y B se hubieran presentado con listas únicas, el reparto de escaños habría variado:
| Partidos: | Partido A | Partido B | Partido C | Partido D | Partido E | Partido F | TOTAL |
|---|---|---|---|---|---|---|---|
| votos: | 33.500 | 21.300 | 34.300 | 4.900 | 4.200 | 1.800 | 100.000 |
| cociente: | 10.000 | ||||||
| escaños por cociente: | 3 | 2 | 3 | 0 | 0 | 0 | 8 |
| votos por cociente: | 30.000 | 20.000 | 30.000 | 0 | 0 | 0 | 80.000 |
| votos de residuo: | 3.500 | 1.300 | 4.300 | 4.900 | 4.200 | 1.800 | 20.000 |
| escaños por residuo: | 0 | 0 | +1 | +1 | 0 | 0 | 2 |
| Total de escaños: | 3 | 2 | 4 | 1 | 0 | 0 | 10 |
El partido A tendría un escaño menos, el cual gana el partido C.
En la práctica es imposible prohibir a un partido dividirse en varios y aunque este sistema inicialmente sobrerrepresenta a los partidos pequeños y perjudica a los grandes, los partidos grandes pueden dividirse en partidos pequeños cuando lo deseen (y de un partido grande salen muchos pequeños, por lo que tendrán ventaja enfrentandose a una cantidad menor de partidos del mismo tamaño) obteniendo una gran ventaja, mayor que si se hubiera utilizado un sistema más equitativo.
jueves, 8 de marzo de 2012
Divisores
Ya hemos hablado de los sistemas "del resto mayor", ahora trataremos los sistemas "del divisor". Estos sistemas se caracterizan por repartir los escaños sin dejar restos, es decir, de un sólo modo.
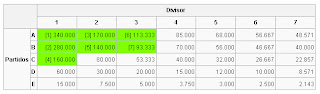
Consisten en dividir los votos de cada partido entre una sucesión de cifras (por ejemplo entre 1, 3, 5....) y seleccionar las cantidades más altas para asignarles los escaños a repartir. Clarificaré está explicación con un ejemplo:
Según el cual, si hubiera 5 partidos con 340.000, 280.000, 160.000, 60.000 y 15.000 votos respectivamente, al repartir 7 escaños con el sistema descrito (dividiendo los votos entre los primeros números impares) le corresponderían 3 al primer partido, 2 al segundo, 1 al tercero y 1 al cuarto. Este sistema recibe el nombre de Sainte-Laguë.
Si hubiéramos utilizado como divisores, en cambio, los primeros números naturales (pares e impares) estaríamos aplicando el método D'Hondt y los resultados serían distintos:
Como puede verse, ahora el reparto de escaños es 3:3:1 en vez de 3:2:1:1, el partido B gana el escaño que pierde D.
Fácilmente puede observarse que existen tantos sistemas de este tipo, como sucesiones de divisores elijas y dependiendo de la relación entre ellos beneficiaran a los grandes o a los pequeños partidos. La sucesión 1,2,4,8... perjudica claramente a los más votados al hacer cada escaño más dificil de obtener que el anterior (prácticamente garantiza un primer escaño a todos en vez de muchos a uno); mientras 100,101,102... beneficia a los más grandes, puesto que en cada división se reducen poco los votos y es posible que el más votado se lleve varios escaños antes de que el segundo partido consiga su primer escaño.
Puedo seguir poniendo ejemplos: 1, 1000, 1001, 1002... (caso extremo en que probablemente todos tendrían un escaño y nadie más de uno); 1,1,1,1,1... (otorga todos los escaños al partido más votado); 1,1, 8, 16, 32... (cada partido obtendrá 2 escaños con pocas posibilidades de obtener alguno más)....
Así que dependiendo de los divisores utilizados obtendremos un resultado u otro. El más representativo de todos estos sistemas es el método D'Hondt, que consigue que cada escaño valga la misma cantidad de votos, por lo que lo estudiaré a fondo en la siguiente entrada. Los demás sistemas desvirtúan la proporción de algún modo.
Añadiré finalmente que los sistemas "del divisor" pueden utilizarse igualmente para asignar escaños a las circunscripciones o distritos electorales, haciendo éstas el papel de los partidos y su población el papel de los votos de cada uno, repartiéndose los escaños totales del Parlamento.
Todos los sistemas "del divisor" están exentos de las paradojas de Alabama, de la población y de las alternativas irrelevantes, ya que si aumentas el número de escaños totales nadie puede perder respecto de un reparto con menos escaños (habrá más zonas coloreadas en verde) ni puede nadie ganar escaños si se reparten menos (algunas de las zonas coloreadas desaparecerán), como tampoco perjudica a ningún partido ganar votos (todos sus cocientes crecerán) ni beneficia perderlos (los cocientes menguarán), tampoco modifica nada el reparto que se añadan a la tabla partidos con menos votos que la última zona coloreada de verde (o sea, partidos que no se lleven ningún escaño).
Consisten en dividir los votos de cada partido entre una sucesión de cifras (por ejemplo entre 1, 3, 5....) y seleccionar las cantidades más altas para asignarles los escaños a repartir. Clarificaré está explicación con un ejemplo:
Según el cual, si hubiera 5 partidos con 340.000, 280.000, 160.000, 60.000 y 15.000 votos respectivamente, al repartir 7 escaños con el sistema descrito (dividiendo los votos entre los primeros números impares) le corresponderían 3 al primer partido, 2 al segundo, 1 al tercero y 1 al cuarto. Este sistema recibe el nombre de Sainte-Laguë.
Si hubiéramos utilizado como divisores, en cambio, los primeros números naturales (pares e impares) estaríamos aplicando el método D'Hondt y los resultados serían distintos:
Como puede verse, ahora el reparto de escaños es 3:3:1 en vez de 3:2:1:1, el partido B gana el escaño que pierde D.
Fácilmente puede observarse que existen tantos sistemas de este tipo, como sucesiones de divisores elijas y dependiendo de la relación entre ellos beneficiaran a los grandes o a los pequeños partidos. La sucesión 1,2,4,8... perjudica claramente a los más votados al hacer cada escaño más dificil de obtener que el anterior (prácticamente garantiza un primer escaño a todos en vez de muchos a uno); mientras 100,101,102... beneficia a los más grandes, puesto que en cada división se reducen poco los votos y es posible que el más votado se lleve varios escaños antes de que el segundo partido consiga su primer escaño.
Puedo seguir poniendo ejemplos: 1, 1000, 1001, 1002... (caso extremo en que probablemente todos tendrían un escaño y nadie más de uno); 1,1,1,1,1... (otorga todos los escaños al partido más votado); 1,1, 8, 16, 32... (cada partido obtendrá 2 escaños con pocas posibilidades de obtener alguno más)....
Así que dependiendo de los divisores utilizados obtendremos un resultado u otro. El más representativo de todos estos sistemas es el método D'Hondt, que consigue que cada escaño valga la misma cantidad de votos, por lo que lo estudiaré a fondo en la siguiente entrada. Los demás sistemas desvirtúan la proporción de algún modo.
Añadiré finalmente que los sistemas "del divisor" pueden utilizarse igualmente para asignar escaños a las circunscripciones o distritos electorales, haciendo éstas el papel de los partidos y su población el papel de los votos de cada uno, repartiéndose los escaños totales del Parlamento.
Todos los sistemas "del divisor" están exentos de las paradojas de Alabama, de la población y de las alternativas irrelevantes, ya que si aumentas el número de escaños totales nadie puede perder respecto de un reparto con menos escaños (habrá más zonas coloreadas en verde) ni puede nadie ganar escaños si se reparten menos (algunas de las zonas coloreadas desaparecerán), como tampoco perjudica a ningún partido ganar votos (todos sus cocientes crecerán) ni beneficia perderlos (los cocientes menguarán), tampoco modifica nada el reparto que se añadan a la tabla partidos con menos votos que la última zona coloreada de verde (o sea, partidos que no se lleven ningún escaño).
lunes, 20 de febrero de 2012
Sistema D'Hondt
Como ya he explicado anteriormente, este sistema es el "del divisor" con los números naturales como divisores.
Para aplicarlo manualmente se puede rellenar una tabla colocando en fila cada partido y debajo de cada uno sus votos, después se colocan en columna los números naturales desde 1 hasta el total de escaños a repartir (se podrían poner también los partidos en columna y los divisores en fila) y se rellenan las casillas con los votos de cada partido dividido entre el número correspondiente -por ejemplo, en la casilla 3B se pone el número de votos del partido B entre 3- para marcar después las casillas en que aparecen los números más grandes de todo el tablero (tantas casillas como escaños a repartir). Cada partido se lleva tantos escaños como casillas tenga marcadas en su columna (el partido A se lleva tantos escaños como casillas marcadas debajo de la casilla 'A'...)
Es evidente que el partido más votado se llevará siempre el primer escaño y por tanto se llevará alguno (es poco frecuente que un sistema electoral deje sin escaños al partido más votado) y no se llevará más de los que se repartan (por ello no hacen falta más columnas).
Puede observarse también que con este sistema un partido con más votos que otro no puede llevarse menos escaños (al tener cocientes mayores, razón que impedía también la paradoja de la población) y que los escaños repartidos pueden numerarse (el primer escaño es el que se adjudica si sólo se repartiera 1; el segundo es, el otro que se adjudica si sólo se repartieran 2... el n-ésimo es de todos los escaños adjudicados el que no estaba cuando se repartían sólo n-1), por esta misma razón no puede darse la paradoja de Alabama. También se observa de este tipo de reparto que un partido que no se lleva ningún escaño no puede influir sobre el reparto, por lo que no se da la paradoja de las alternativas irrelevantes.
Otro tipo de reparto manual, con el mismo resultado, consistiría en colocar debajo de cada partido su número de votos (de momento sólo escribimos la primera fila) y seleccionamos la casilla con el número más grande, después de asignarle un escaño al partido correspondiente, dividimos sus votos entre 2 y miramos cual es el número más grande de los que hay ahora (si es la casilla de otro partido dividimos sus votos entre 2, si es el mismo partido dividimos entre 3), repitiendo el proceso hasta asignar todos los escaños. Es una forma de ahorrarse divisiones innecesarias, ya que una cantidad dividida entre otra es más grande que si se divide esa misma cantidad entre un divisor mayor, es decir, si no te corresponde un escaño por tus votos tampoco lo tendrás por la mitad o un tercio de ellos. Para resolver los empates entre casillas suele adjudicarse el escaño al partido más votado, o en caso de nuevo empate, se sortea de algún modo.
Hasta aquí, todas las propiedades analizadas son comunes a todos los sistemas "del divisor", pero el método D'Hondt tiene alguna más. La más importante de todas es que otorga a cada escaño el mismo valor en votos, veamoslo:
La última casilla marcada, es decir, la de menor número dentro de todas las marcadas contiene lo que se denomina "la cifra distribuidora", ese número es el coste del escaño (de tal modo que se repartan todos y no falte ninguno). Observese que ese número es mayor que los no marcados y es el menor de los marcados, por lo que si se le otorga a cada escaño ese valor en votos, cada partido obtendrá los escaños que aparecen en el gráfico (lo que implica que se reparten exactamente los que se querían repartir), siendo los restos inferiores al coste de escaño.
Podemos comprobarlo en el ejemplo concreto que hemos puesto: el coste del escaño es de 93.333 votos, B obtiene 3 escaños (porque la casilla B3 tiene un tercio de los votos obtenidos por B), A obtiene otros 3 (no puede tener 4 porque entonces la "cifra distribuidora" habría sido la de la casilla A4 y no la B3, sin embargo como A tiene más votos que B sus cocientes son más grandes y debe tener al menos 3 escaños), por último C tiene 1 escaño, al ser un número mayor que 93.333, pero no puede tener 2, por que entonces la mitad debería ser mayor que 93.333 y sería la "cifra distribuidora". Por último, 340.000 = 93.333*3 + 61.000, 280.000 = 93.333*3 + 1 y 160.000= 93.333*1 + 66.667; es decir, 3 escaños para A, 3 para B y 1 para C, quedando los restos (61.000, 1, 66.667) menores que la "cifra distribuidora" -ya que el resto siempre es menor que el divisor- y los restos de los que no lograron escaño (60.000, 15.000) deben ser también menores, porque de otro modo serían superiores a la "cifra distribuidora" y estarían remarcados.
Este hecho tiene mayor trascendencia de lo que parece, puesto que el algoritmo descrito para repartir escaños por el método D'Hondt es factible en todos los casos, implica que siempre hay una "cifra distribuidora", o sea, siempre se puede encontrar un precio por escaño (igual para todos los escaños) tal que se repartan todos los escaños (ni uno más ni uno menos) y de tal modo que los restos sean inferiores al precio del escaño.
Además, no puede existir otro reparto distinto de escaños que cumpla la misma propiedad (equitatividad del coste de los escaños), porque si existiera llegaríamos a una contradicción:
Un reparto distinto de los escaños quiere decir que al menos un partido tiene algún escaño menos que con el otro sistema (si nadie tiene un escaño menos tampoco nadie puede tener un escaño más -ya que el total de los escaños repartidos ha de ser el mismo, o sea, la suma de los escaños de cada partido- y entonces el reparto de escaños sería el mismo) y al menos otro partido ha de tener algún escaño más (por el mismo razonamiento). Si el coste de escaños es 'X' con el método D'Hondt y 'Z' con el nuevo sistema de reparto, 'X' no puede ser igual a 'Z', porque habría producido el mismo reparto; si 'X' es menor que 'Z', tomemos uno de los partidos que tienen más escaños con el nuevo sistema y dividamoslo entre 'X', tiene que dar un cociente igual o mayor que dividido entre 'Z' y sin embargo hemos dicho que con D'Hondt ese partido tenía menos escaños, o sea, que daba menos dividido entre 'X', lo que implica contradicción. Se llega a una contradicción parecida si 'X' es mayor que 'Z', tomando un partido que tenga menos escaños con el nuevo sistema.
Hemos logrado con esto un método que nos otorga siempre un reparto de escaños (que existe y es único) con equitatividad del coste del escaño. Aunque la "cifra distribuidora" no es única, en realidad hay todo un intervalo dentro del cual vale cualquier número para que el reparto de escaños (que es lo que nos importa) sea el mismo. Un número más grande que los del intervalo nos daría un reparto en el que sobran escaños sin repartir y uno más pequeño haría que se repartiesen más escaños de los que hay. El intervalo es (k,m] donde k es la última cifra verde para repartir n+1 escaños (k o un número menor repartiría más de n escaños) y m la de repartir n escaños (un número mayor repartiría menos de n escaños), suele tomarse m como cifra distribuidora para simplificar los cálculos. En nuestro ejemplo el intervalo es (85.000, 93.333] y como puede verse un numero mayor de 93.333 le quitaría a B su tercer escaño y 85.000 o un número menor le daría a A el cuarto.
El algoritmo manual que he descrito (con sus dos variantes) nos proporciona una de las posibles "cifras distribuidoras" y el único reparto de escaños posible, pero hallar directamente una "cifra distribuidora" a base de elegir un número al azar y subirlo o bajarlo hasta entrar en el intervalo en el que se reparte el número exacto de escaños que queremos nos daría el mismo reparto y sería otra forma de implementar D'Hondt, un algoritmo mecánico, como el que he programado yo en código 'C', programa que estoy dispuesto a compartir con quien lo desee, muy útil para simulaciones por ordenador o conteo automático de escaños.
Debido a las propiedades de este sistema, muchos países lo han adoptado para sus elecciones legislativas, pero algunos de ello lo han "corregido" de múltiples formas, como es el caso de España que lo utiliza para las elecciones municipales, regionales, al congreso nacional y europeas. Por ello en la siguiente entrada trataré correcciones reales aplicadas a este sistema electoral.
Para aplicarlo manualmente se puede rellenar una tabla colocando en fila cada partido y debajo de cada uno sus votos, después se colocan en columna los números naturales desde 1 hasta el total de escaños a repartir (se podrían poner también los partidos en columna y los divisores en fila) y se rellenan las casillas con los votos de cada partido dividido entre el número correspondiente -por ejemplo, en la casilla 3B se pone el número de votos del partido B entre 3- para marcar después las casillas en que aparecen los números más grandes de todo el tablero (tantas casillas como escaños a repartir). Cada partido se lleva tantos escaños como casillas tenga marcadas en su columna (el partido A se lleva tantos escaños como casillas marcadas debajo de la casilla 'A'...)
Es evidente que el partido más votado se llevará siempre el primer escaño y por tanto se llevará alguno (es poco frecuente que un sistema electoral deje sin escaños al partido más votado) y no se llevará más de los que se repartan (por ello no hacen falta más columnas).
Puede observarse también que con este sistema un partido con más votos que otro no puede llevarse menos escaños (al tener cocientes mayores, razón que impedía también la paradoja de la población) y que los escaños repartidos pueden numerarse (el primer escaño es el que se adjudica si sólo se repartiera 1; el segundo es, el otro que se adjudica si sólo se repartieran 2... el n-ésimo es de todos los escaños adjudicados el que no estaba cuando se repartían sólo n-1), por esta misma razón no puede darse la paradoja de Alabama. También se observa de este tipo de reparto que un partido que no se lleva ningún escaño no puede influir sobre el reparto, por lo que no se da la paradoja de las alternativas irrelevantes.
Otro tipo de reparto manual, con el mismo resultado, consistiría en colocar debajo de cada partido su número de votos (de momento sólo escribimos la primera fila) y seleccionamos la casilla con el número más grande, después de asignarle un escaño al partido correspondiente, dividimos sus votos entre 2 y miramos cual es el número más grande de los que hay ahora (si es la casilla de otro partido dividimos sus votos entre 2, si es el mismo partido dividimos entre 3), repitiendo el proceso hasta asignar todos los escaños. Es una forma de ahorrarse divisiones innecesarias, ya que una cantidad dividida entre otra es más grande que si se divide esa misma cantidad entre un divisor mayor, es decir, si no te corresponde un escaño por tus votos tampoco lo tendrás por la mitad o un tercio de ellos. Para resolver los empates entre casillas suele adjudicarse el escaño al partido más votado, o en caso de nuevo empate, se sortea de algún modo.
Hasta aquí, todas las propiedades analizadas son comunes a todos los sistemas "del divisor", pero el método D'Hondt tiene alguna más. La más importante de todas es que otorga a cada escaño el mismo valor en votos, veamoslo:
La última casilla marcada, es decir, la de menor número dentro de todas las marcadas contiene lo que se denomina "la cifra distribuidora", ese número es el coste del escaño (de tal modo que se repartan todos y no falte ninguno). Observese que ese número es mayor que los no marcados y es el menor de los marcados, por lo que si se le otorga a cada escaño ese valor en votos, cada partido obtendrá los escaños que aparecen en el gráfico (lo que implica que se reparten exactamente los que se querían repartir), siendo los restos inferiores al coste de escaño.
Podemos comprobarlo en el ejemplo concreto que hemos puesto: el coste del escaño es de 93.333 votos, B obtiene 3 escaños (porque la casilla B3 tiene un tercio de los votos obtenidos por B), A obtiene otros 3 (no puede tener 4 porque entonces la "cifra distribuidora" habría sido la de la casilla A4 y no la B3, sin embargo como A tiene más votos que B sus cocientes son más grandes y debe tener al menos 3 escaños), por último C tiene 1 escaño, al ser un número mayor que 93.333, pero no puede tener 2, por que entonces la mitad debería ser mayor que 93.333 y sería la "cifra distribuidora". Por último, 340.000 = 93.333*3 + 61.000, 280.000 = 93.333*3 + 1 y 160.000= 93.333*1 + 66.667; es decir, 3 escaños para A, 3 para B y 1 para C, quedando los restos (61.000, 1, 66.667) menores que la "cifra distribuidora" -ya que el resto siempre es menor que el divisor- y los restos de los que no lograron escaño (60.000, 15.000) deben ser también menores, porque de otro modo serían superiores a la "cifra distribuidora" y estarían remarcados.
Este hecho tiene mayor trascendencia de lo que parece, puesto que el algoritmo descrito para repartir escaños por el método D'Hondt es factible en todos los casos, implica que siempre hay una "cifra distribuidora", o sea, siempre se puede encontrar un precio por escaño (igual para todos los escaños) tal que se repartan todos los escaños (ni uno más ni uno menos) y de tal modo que los restos sean inferiores al precio del escaño.
Además, no puede existir otro reparto distinto de escaños que cumpla la misma propiedad (equitatividad del coste de los escaños), porque si existiera llegaríamos a una contradicción:
Un reparto distinto de los escaños quiere decir que al menos un partido tiene algún escaño menos que con el otro sistema (si nadie tiene un escaño menos tampoco nadie puede tener un escaño más -ya que el total de los escaños repartidos ha de ser el mismo, o sea, la suma de los escaños de cada partido- y entonces el reparto de escaños sería el mismo) y al menos otro partido ha de tener algún escaño más (por el mismo razonamiento). Si el coste de escaños es 'X' con el método D'Hondt y 'Z' con el nuevo sistema de reparto, 'X' no puede ser igual a 'Z', porque habría producido el mismo reparto; si 'X' es menor que 'Z', tomemos uno de los partidos que tienen más escaños con el nuevo sistema y dividamoslo entre 'X', tiene que dar un cociente igual o mayor que dividido entre 'Z' y sin embargo hemos dicho que con D'Hondt ese partido tenía menos escaños, o sea, que daba menos dividido entre 'X', lo que implica contradicción. Se llega a una contradicción parecida si 'X' es mayor que 'Z', tomando un partido que tenga menos escaños con el nuevo sistema.
Hemos logrado con esto un método que nos otorga siempre un reparto de escaños (que existe y es único) con equitatividad del coste del escaño. Aunque la "cifra distribuidora" no es única, en realidad hay todo un intervalo dentro del cual vale cualquier número para que el reparto de escaños (que es lo que nos importa) sea el mismo. Un número más grande que los del intervalo nos daría un reparto en el que sobran escaños sin repartir y uno más pequeño haría que se repartiesen más escaños de los que hay. El intervalo es (k,m] donde k es la última cifra verde para repartir n+1 escaños (k o un número menor repartiría más de n escaños) y m la de repartir n escaños (un número mayor repartiría menos de n escaños), suele tomarse m como cifra distribuidora para simplificar los cálculos. En nuestro ejemplo el intervalo es (85.000, 93.333] y como puede verse un numero mayor de 93.333 le quitaría a B su tercer escaño y 85.000 o un número menor le daría a A el cuarto.
El algoritmo manual que he descrito (con sus dos variantes) nos proporciona una de las posibles "cifras distribuidoras" y el único reparto de escaños posible, pero hallar directamente una "cifra distribuidora" a base de elegir un número al azar y subirlo o bajarlo hasta entrar en el intervalo en el que se reparte el número exacto de escaños que queremos nos daría el mismo reparto y sería otra forma de implementar D'Hondt, un algoritmo mecánico, como el que he programado yo en código 'C', programa que estoy dispuesto a compartir con quien lo desee, muy útil para simulaciones por ordenador o conteo automático de escaños.
Debido a las propiedades de este sistema, muchos países lo han adoptado para sus elecciones legislativas, pero algunos de ello lo han "corregido" de múltiples formas, como es el caso de España que lo utiliza para las elecciones municipales, regionales, al congreso nacional y europeas. Por ello en la siguiente entrada trataré correcciones reales aplicadas a este sistema electoral.
domingo, 19 de febrero de 2012
Correcciones
Muchas veces a la hora de aplicar un sistema electoral se introducen correcciones o modificaciones para que el resultado sea diferente.
Las correciones son muy variadas y pueden consistir en: eliminar a los minoritarios, garantizarles algún puesto, favorecer al ganador, premiar el voto concentrado en una pequeña zona, castigarlo...
Son buenos ejemplos de correcciones las barreras, o sea, eliminar a todo el que no llegue a un mínimo, ya sea un porcentaje a nivel global o en una circunscripción, presencia relevante en varias circunscripciones, el requisito de haber logrado buen resultado en elecciones anteriores o una cantidad de firmas o de dinero para poder participar en las elecciones, límites de edad...
Más concretamente, en Kirguizistan se exige aprobar un examen de kirguís (lengua oficial), tener entre 35 y 65 años de edad, presentar 30.000 firmas de las cuales deben provenir al menos un 3% de cada uno de los ocho territorios del estado y pagar una fianza de mil veces el salario mínimo mensual que será devuelta sólo si se obtiene al menos 10% de los votos. Para las elecciones parlamentarias se exige a los partidos un aval de 15.000 dólares, que se devolveran si consiguen algún escaño, además hace falta un 0,5% de los votos en cada región y 5% en toda la nación.
También se pueden hacer correcciones en el sentido contrario, tomar un sistema mayoritario y modificarlo para representar a minorías, como es el caso del Senado español (más adelante analizaré detenidamente las listas abiertas) donde el partido mayoritario en cada circunscripción obtiene todos los escaños menos uno, que va para el segundo partido (salvo en Ibiza-Formentera, Menorca, Fuerteventura, Gomera, Hierro, Lanzarote y La Palma en las que hay un sólo escaño, para el partido ganador; y en Ceuta y Melilla donde hay dos escaños, ambos para el ganador), mientras que en un sistema mayoritario sin correcciones todos los escaños son para el ganador.
En Italia, para asegurar la mayoría absoluta, otorgan siempre al ganador el 55% de los escaños y reparten los demás de forma proporcional entre el resto (siempre que superen una barrera mínima del 4% en el Congreso y 8% en el Senado). Pero es mejor que lo explique el primer ministro italiano:
Las correciones son muy variadas y pueden consistir en: eliminar a los minoritarios, garantizarles algún puesto, favorecer al ganador, premiar el voto concentrado en una pequeña zona, castigarlo...
Son buenos ejemplos de correcciones las barreras, o sea, eliminar a todo el que no llegue a un mínimo, ya sea un porcentaje a nivel global o en una circunscripción, presencia relevante en varias circunscripciones, el requisito de haber logrado buen resultado en elecciones anteriores o una cantidad de firmas o de dinero para poder participar en las elecciones, límites de edad...
Más concretamente, en Kirguizistan se exige aprobar un examen de kirguís (lengua oficial), tener entre 35 y 65 años de edad, presentar 30.000 firmas de las cuales deben provenir al menos un 3% de cada uno de los ocho territorios del estado y pagar una fianza de mil veces el salario mínimo mensual que será devuelta sólo si se obtiene al menos 10% de los votos. Para las elecciones parlamentarias se exige a los partidos un aval de 15.000 dólares, que se devolveran si consiguen algún escaño, además hace falta un 0,5% de los votos en cada región y 5% en toda la nación.
También se pueden hacer correcciones en el sentido contrario, tomar un sistema mayoritario y modificarlo para representar a minorías, como es el caso del Senado español (más adelante analizaré detenidamente las listas abiertas) donde el partido mayoritario en cada circunscripción obtiene todos los escaños menos uno, que va para el segundo partido (salvo en Ibiza-Formentera, Menorca, Fuerteventura, Gomera, Hierro, Lanzarote y La Palma en las que hay un sólo escaño, para el partido ganador; y en Ceuta y Melilla donde hay dos escaños, ambos para el ganador), mientras que en un sistema mayoritario sin correcciones todos los escaños son para el ganador.
En Italia, para asegurar la mayoría absoluta, otorgan siempre al ganador el 55% de los escaños y reparten los demás de forma proporcional entre el resto (siempre que superen una barrera mínima del 4% en el Congreso y 8% en el Senado). Pero es mejor que lo explique el primer ministro italiano:
En España se ha modificado el sistema D'Hondt dividiendo la nación en 52 circunscripciones entre las cuales se dividen los 350 escaños con el método Hare y se aplica el sistema D'Hondt a cada circunscripción, con una barrera del 3% de los votos en cada una. De este modo se premia el voto concentrado en pocos distritos frente al voto disperso en muchos. Quiere decir esto que es preferible obtener el 30% de los votos en una provincia que 2,9% en todas ellas (que sería como no tener nada).
En cambio, otros sistemas penalizan la concentración del voto, como es el caso del sistema peruano; donde para no quedar fuera del congreso se requiere obtener 6 escaños en al menos 2 distritos distintos, o un 5% de los votos a nivel nacional.
Como puede entenderse, las correcciones modifican el sistema electoral escogido, con lo que pueden perderse algunas de sus propiedades. Me centraré en la próxima entrada en el sistema electoral español, que he tocado aquí de pasada, para explicar por qué no ocurre lo que el sistema d'Hondt en anteriores entradas garantizaba.
sábado, 18 de febrero de 2012
Elección del Congreso español
Como he adelantado en entradas anteriores, se trata de un procedimiento complejo. En primer lugar se dividen los 350 escaños de los que se compone la cámara, asignando uno a Ceuta, otro a Melilla y dos a cada provincia inicialmente, para después repartir el resto (248) entre todas las provincias en función de su población, aplicando el método Hare. Este es el reparto para las elecciones de 2011:
Después se reparten los escaños de cada provincia, usando el método D'Hondt, entre los partidos que han superado el 3% de los votos válidos emitidos en cada una.
Puede entreverse ahora por qué esta elección no es proporcional, pese a usar un sistema como D'Hondt:
1. Existen varias circunscripciones o distritos entre los que se dividen los escaños.
2. Se reparten a priori una centena de escaños a las provincias de forma equitativa, no proporcional a la población.
3. Los demás escaños se reparten con un sistema "proporcional" corregido, Hare, que sobrerrepresenta a las provincias menos pobladas.
4. Existe una barrera en cada provincia del 3 % de los votos válidos emitidos en ella.
Todo ello modifica sensiblemente el resultado como puede observarse:
A la derecha figuran los escaños obtenidos realmente y a la izquierda los que se habrían logrado si cada escaño valiese lo mismo (66.040 votos).
Esto se debe fundamentalmente a la primera medida, la multiplicidad de circunscripciones, que actúa como una reducción de los escaños elegibles. Suponiendo que todas las provincias fueran igualmente pobladas y que cada partido tuviera sus votos equitativamente distribuidos en todas ellas, el resultado es el mismo que el de repartir proporcionalmente sólo los escaños que corresponden a cada provincia y luego multiplicar por el número de provincias, en vez de repartir proporcionalmente los escaños totales.
Para que se entienda mejor pondré un ejemplo ficticio:
El partido A obtiene 1.000.000 de votos, el B 900.000, el C 200.000, el D 50.000, el E 5.000....
Si se reparte un sólo escaño se lo llevará el más votado; si se reparten 3, serán 2 para A y 1 para B; si se reparten 11, el reparto quedará en 5, 5 y 1 (ya entra C); para que entrase D se necesitarían 43 escaños; 431 para que entrase E... La proporcionalidad aumenta al aumentar el número de escaños a repartir (repartir un sólo escaño o tantos como votos haya, son casos extremos que nos llevan a un sistema mayoritario estricto donde sólo tiene escaño el más votado o a un sistema de proporción total).
Repartir 600 escaños pero en 200 distritos (suponiendo que estén igual de poblados y el voto de cada partido igualmente distribuido en ellos) supondría repartir 3 escaños 200 veces, es decir, 400 (200 X 2) para A y 200 (200 X 1) para B. Como puede verse, la existencia de circunscripciones reduce la proporción, como si el número de escaños a repartir fuera en realidad menor.
En el caso español, se reparten 350 escaños en 52 circunscripciones, por lo que se reparten casi 7 escaños de media. Con el ejemplo anterior de voto igualmente distribuido y circunscripciones igualmente pobladas, el resultado sería 4/7 de los escaños para PP y 3/7 para PSOE, es decir, 200 y 150 respectivamente.
Si el resultado no ha sido así es porque no se cumplen esas dos hipótesis. Existen en España provincias muy pobladas, como Madrid o Barcelona que reparten más de 30 escaños mientras otras muchas reparten menos de 5. Gracias a las grandes circunscripciones se logra ganar un poco de proporcionalidad, porque ya empiezan a conseguir escaños los terceros y cuartos partidos.
Aquí es donde entran en juego los puntos 2 y 3. Para impedir que haya provincias con muchos escaños y otras con muy pocos, se sobrerrepresenta a las menos pobladas, quitandole bastantes escaños a unas pocas y dandole uno o dos escaños más a muchas, cosa que empeora la proprocionalidad de los partidos, ya que 4 escaños suelen ser tan pocos como 2 para que aparezcan más partidos en el reparto, mientras bajar de 45 a 35 escaños supone realmente una pérdida para los minoritarios.
Por último, en aquellas circunscripciones que después de todo pasan de 30 escaños, la barrera del 3% impide que los partidos más pequeños accedan al reparto de los mismos, por muy proporcional que sea luego la distribución entre los que pasen la barrera.
Se comprende bien ahora cómo el reparto proporcional de unos pocos escaños no arroja un resultado similar al reparto proporcional de 350 escaños (que sería el equivalente a usar D'Hondt en circunscripción única y sin la barrera del 3% mínimo). Es decir, un sistema proporcional puede dejar de serlo al aplicarle suficientes correcciones.
En el caso español han salido perjudicados: PACMA (-100%), PA (-100%), Eb (-100%), EQUO (-100%), UPyD (-70,59%) e IU (-56%).
Y beneficiados: G-Bai (+∞%), EAJ-PNV (+25%), AMAIUR (+40%), CiU (+6,66%), PSOE (+4,76%) y PP (+13,41%).
Como se apreciaba intuitivamente, han salido perdiendo los pequeños y medianos partidos que tienen su voto disperso por toda España, se han mantenido los partidos pequeños con el voto concentrado en una zona y han salido beneficiados los dos grandes partidos españoles y sobre todo los medianos partidos con el voto concentrado en una zona o los partidos minúsculos pero que tienen su voto aún más concentrado (como es el caso de G-Bai que cuenta sólo con el 0,17% de los votos pero todos ellos en la poco poblada Navarra).
El motivo por el que CiU no está excesivamente sobrerrepresentado es porque una de las 4 provincias en las que acumula sus votos es la inmensa Barcelona (la segunda más poblada, con 31 escaños), en la que el reparto de escaños es bastante proporcional.
Si considerasemos CiU como un partido en Barcelona y otro distinto en las otras provincias habría sacado:
305.040 votos y 7 escaños en Lérida, Tarragona y Gerona, mereciendo 4 (+75%).
709.223 votos y 9 escaños en Barcelona, mereciendo 11 (-18,18%).
Es decir, el sistema electoral español no sólo beneficia a los dos grandes partidos, sino también a los partidos que concentran su voto en una región (sobre todo si es pequeña), en detrimento de todos los demás partidos.
Después se reparten los escaños de cada provincia, usando el método D'Hondt, entre los partidos que han superado el 3% de los votos válidos emitidos en cada una.
Puede entreverse ahora por qué esta elección no es proporcional, pese a usar un sistema como D'Hondt:
1. Existen varias circunscripciones o distritos entre los que se dividen los escaños.
2. Se reparten a priori una centena de escaños a las provincias de forma equitativa, no proporcional a la población.
3. Los demás escaños se reparten con un sistema "proporcional" corregido, Hare, que sobrerrepresenta a las provincias menos pobladas.
4. Existe una barrera en cada provincia del 3 % de los votos válidos emitidos en ella.
Todo ello modifica sensiblemente el resultado como puede observarse:
Esto se debe fundamentalmente a la primera medida, la multiplicidad de circunscripciones, que actúa como una reducción de los escaños elegibles. Suponiendo que todas las provincias fueran igualmente pobladas y que cada partido tuviera sus votos equitativamente distribuidos en todas ellas, el resultado es el mismo que el de repartir proporcionalmente sólo los escaños que corresponden a cada provincia y luego multiplicar por el número de provincias, en vez de repartir proporcionalmente los escaños totales.
Para que se entienda mejor pondré un ejemplo ficticio:
El partido A obtiene 1.000.000 de votos, el B 900.000, el C 200.000, el D 50.000, el E 5.000....
Si se reparte un sólo escaño se lo llevará el más votado; si se reparten 3, serán 2 para A y 1 para B; si se reparten 11, el reparto quedará en 5, 5 y 1 (ya entra C); para que entrase D se necesitarían 43 escaños; 431 para que entrase E... La proporcionalidad aumenta al aumentar el número de escaños a repartir (repartir un sólo escaño o tantos como votos haya, son casos extremos que nos llevan a un sistema mayoritario estricto donde sólo tiene escaño el más votado o a un sistema de proporción total).
Repartir 600 escaños pero en 200 distritos (suponiendo que estén igual de poblados y el voto de cada partido igualmente distribuido en ellos) supondría repartir 3 escaños 200 veces, es decir, 400 (200 X 2) para A y 200 (200 X 1) para B. Como puede verse, la existencia de circunscripciones reduce la proporción, como si el número de escaños a repartir fuera en realidad menor.
En el caso español, se reparten 350 escaños en 52 circunscripciones, por lo que se reparten casi 7 escaños de media. Con el ejemplo anterior de voto igualmente distribuido y circunscripciones igualmente pobladas, el resultado sería 4/7 de los escaños para PP y 3/7 para PSOE, es decir, 200 y 150 respectivamente.
Si el resultado no ha sido así es porque no se cumplen esas dos hipótesis. Existen en España provincias muy pobladas, como Madrid o Barcelona que reparten más de 30 escaños mientras otras muchas reparten menos de 5. Gracias a las grandes circunscripciones se logra ganar un poco de proporcionalidad, porque ya empiezan a conseguir escaños los terceros y cuartos partidos.
Aquí es donde entran en juego los puntos 2 y 3. Para impedir que haya provincias con muchos escaños y otras con muy pocos, se sobrerrepresenta a las menos pobladas, quitandole bastantes escaños a unas pocas y dandole uno o dos escaños más a muchas, cosa que empeora la proprocionalidad de los partidos, ya que 4 escaños suelen ser tan pocos como 2 para que aparezcan más partidos en el reparto, mientras bajar de 45 a 35 escaños supone realmente una pérdida para los minoritarios.
Por último, en aquellas circunscripciones que después de todo pasan de 30 escaños, la barrera del 3% impide que los partidos más pequeños accedan al reparto de los mismos, por muy proporcional que sea luego la distribución entre los que pasen la barrera.
Se comprende bien ahora cómo el reparto proporcional de unos pocos escaños no arroja un resultado similar al reparto proporcional de 350 escaños (que sería el equivalente a usar D'Hondt en circunscripción única y sin la barrera del 3% mínimo). Es decir, un sistema proporcional puede dejar de serlo al aplicarle suficientes correcciones.
En el caso español han salido perjudicados: PACMA (-100%), PA (-100%), Eb (-100%), EQUO (-100%), UPyD (-70,59%) e IU (-56%).
Y beneficiados: G-Bai (+∞%), EAJ-PNV (+25%), AMAIUR (+40%), CiU (+6,66%), PSOE (+4,76%) y PP (+13,41%).
Como se apreciaba intuitivamente, han salido perdiendo los pequeños y medianos partidos que tienen su voto disperso por toda España, se han mantenido los partidos pequeños con el voto concentrado en una zona y han salido beneficiados los dos grandes partidos españoles y sobre todo los medianos partidos con el voto concentrado en una zona o los partidos minúsculos pero que tienen su voto aún más concentrado (como es el caso de G-Bai que cuenta sólo con el 0,17% de los votos pero todos ellos en la poco poblada Navarra).
El motivo por el que CiU no está excesivamente sobrerrepresentado es porque una de las 4 provincias en las que acumula sus votos es la inmensa Barcelona (la segunda más poblada, con 31 escaños), en la que el reparto de escaños es bastante proporcional.
Si considerasemos CiU como un partido en Barcelona y otro distinto en las otras provincias habría sacado:
305.040 votos y 7 escaños en Lérida, Tarragona y Gerona, mereciendo 4 (+75%).
709.223 votos y 9 escaños en Barcelona, mereciendo 11 (-18,18%).
Es decir, el sistema electoral español no sólo beneficia a los dos grandes partidos, sino también a los partidos que concentran su voto en una región (sobre todo si es pequeña), en detrimento de todos los demás partidos.
viernes, 17 de febrero de 2012
Bolsa de restos
En algunas ocasiones se han propuesto sistemas electorales supuestamente equivalentes al reparto equitativo puro (en el que todo escaño vale la misma cantidad de votos), con la intención de cumplir alguna propiedad más, como puede ser el hecho de representar también a los territorios (implantando varias circunscripciones) o elegir a una sola persona y no a varias (haciendo que dichas circunscripciones sean uninominales).
Un sistema mixto, en que se elijan parte de los representantes en varios distritos y parte a nivel global, evidentemente no cumple la propiedad buscada de proporcionalidad. Basta ver como, después de hacer el reparto global, añadir los escaños procedentes de los distritos distorsiona la proporción (incluso hacer dos veces el reparto global, duplicando los escaños, ya hemos visto en la entrada anterior que perjudica la proporción también reduciéndola a la que se obtendría con una cámara con la mitad de escaños).
Uno de estos sistemas que pretende ser proporcional es una modificación del sistema anterior añadiendo una "bolsa de restos". Consiste en tomar los restos de cada partido en todos los distritos (la suma de los votos que han sobrado tras el reparto de escaños) y usar ese número de votos como la cifra que llevará cada partido al distrito global (en vez acudir al distrito global con todos los votos) en el que se repartirán los demás escaños.
Sin embargo, este sistema no otorga el mismo valor a cada escaño, aunque pudiera parecerlo a priori. Basta suponer que tenemos dos distritos (J y K) para construir un ejemplo en el que no se cumple:
Se reparten 6 escaños en el distrito J y 4 en el distrito K, después se asignarán 10 más a nivel global en función de los restos. Se han presentado 4 partidos (A, B, C y D).
El escaño ha valido 3050 votos en J y 430 en K. Ahora vamos con los restos.
En esta ocasión el escaño vale 560 votos. Al final los escaños han quedado así:
A: 2+1+4 = 7
B: 1+1+2 = 4
C: 1+1+4 = 6
D: 2+1+0 = 3
Mientras que un reparto equitativo (el escaño vale 1227 votos) dejaría el siguiente resultado:
Creo que se percibe bien la desproporción que supondría otorgarle a C el doble de escaños que a D, teniendo menos votos. La desproporción se debe a que hay X+1 precios del escaño (X es el número de distritos) en vez de un precio único. Se puede afinar la "aproximación" tomando en todos los distritos un valor único del escaño, el menor de los valores de todos los distritos. Repetiremos el reparto anterior tomando 430 como valor del escaño en J y en K.
Ahora repartimos 10 escaños con los nuevos restos.
En esta ocasión el escaño vale 1877 votos. Al final los escaños han quedado así:
A: 2+1+4 = 7
B: 1+1+2 = 4
C: 1+1+2 = 4
D: 2+1+2 = 5
Este reparto se aproxima más (en este caso coincide) al resultado buscado que el anterior, debido a que sólo usamos 2 precios distintos para el escaño en vez de X+1 lo que distorsiona menos la proporción (y eso que en el ejemplo X+1 es 3 tan sólo).
Este caso especial y mejorado de la "bolsa de restos" tampoco coincide necesariamente con un reparto equitativo. Vamos a ver un nuevo ejemplo sobre la bolsa de restos, para constatarlo. Tomaremos 3 partidos (A, B y C) y 2 distritos (J y K).
Hasta ahora A ha obtenido 3 escaños y B 2. En J el escaño vale 20 votos y en K vale 1001.
Veamos los que obtienen gracias a la bolsa de restos (suponemos que en el distrito global se reparten 5 escaños, tantos como la suma de los dos distritos):
Veamos también el reparto de los restos asignando a los escaños un valor de 20 votos en J y K (caso mejorado de la bolsa de restos).
Y por último, el reparto de 10 escaños en un sólo distrito (el caso equitativo en que cada escaño vale 501 votos):
Comparemos los tres repartos:
Como puede observarse, ni con la mejora aplicada a la bolsa de restos (tomar 2 precios distintos del escaño en vez de X+1) se logra imitar el reparto equitativo, aunque resulta más desproporcionado aún el reparto con 3 precios distintos para el escaño. En la siguiente entrada seguiremos analizando sistemas electorales supuestamente equivalentes al reparto equitativo puro, que engañan a la intuición incluso más que el de la bolsa de restos.
Un sistema mixto, en que se elijan parte de los representantes en varios distritos y parte a nivel global, evidentemente no cumple la propiedad buscada de proporcionalidad. Basta ver como, después de hacer el reparto global, añadir los escaños procedentes de los distritos distorsiona la proporción (incluso hacer dos veces el reparto global, duplicando los escaños, ya hemos visto en la entrada anterior que perjudica la proporción también reduciéndola a la que se obtendría con una cámara con la mitad de escaños).
Uno de estos sistemas que pretende ser proporcional es una modificación del sistema anterior añadiendo una "bolsa de restos". Consiste en tomar los restos de cada partido en todos los distritos (la suma de los votos que han sobrado tras el reparto de escaños) y usar ese número de votos como la cifra que llevará cada partido al distrito global (en vez acudir al distrito global con todos los votos) en el que se repartirán los demás escaños.
Sin embargo, este sistema no otorga el mismo valor a cada escaño, aunque pudiera parecerlo a priori. Basta suponer que tenemos dos distritos (J y K) para construir un ejemplo en el que no se cumple:
Se reparten 6 escaños en el distrito J y 4 en el distrito K, después se asignarán 10 más a nivel global en función de los restos. Se han presentado 4 partidos (A, B, C y D).
D’Hondt | A | B | C | D |
Votos | 8000 | 4300 | 5200 | 6100 |
Escaños | 2 | 1 | 1 | 2 |
Resto | 1900 | 1250 | 2150 | 0 |
| D’Hondt | A | B | C | D |
| Votos | 800 | 610 | 520 | 430 |
| Escaños | 1 | 1 | 1 | 1 |
| Resto | 370 | 180 | 90 | 0 |
El escaño ha valido 3050 votos en J y 430 en K. Ahora vamos con los restos.
| D’Hondt | A | B | C | D |
| Votos | 2270 | 1430 | 2240 | 0 |
| Escaños | 4 | 2 | 4 | 0 |
| Resto | 30 | 310 | 0 | 0 |
En esta ocasión el escaño vale 560 votos. Al final los escaños han quedado así:
A: 2+1+4 = 7
B: 1+1+2 = 4
C: 1+1+4 = 6
D: 2+1+0 = 3
Mientras que un reparto equitativo (el escaño vale 1227 votos) dejaría el siguiente resultado:
| D’Hondt | A | B | C | D |
| Votos | 8800 | 4910 | 5720 | 6530 |
| Escaños | 7 | 4 | 4 | 5 |
| Resto | 211 | 2 | 812 | 395 |
Creo que se percibe bien la desproporción que supondría otorgarle a C el doble de escaños que a D, teniendo menos votos. La desproporción se debe a que hay X+1 precios del escaño (X es el número de distritos) en vez de un precio único. Se puede afinar la "aproximación" tomando en todos los distritos un valor único del escaño, el menor de los valores de todos los distritos. Repetiremos el reparto anterior tomando 430 como valor del escaño en J y en K.
D’Hondt | A | B | C | D |
Votos | 8000 | 4300 | 5200 | 6100 |
Escaños | 2 | 1 | 1 | 2 |
Resto | 7140 | 3870 | 4770 | 5240 |
| D’Hondt | A | B | C | D |
| Votos | 800 | 610 | 520 | 430 |
| Escaños | 1 | 1 | 1 | 1 |
| Resto | 370 | 180 | 90 | 0 |
Ahora repartimos 10 escaños con los nuevos restos.
| D’Hondt | A | B | C | D |
| Votos | 7510 | 4050 | 4860 | 5240 |
| Escaños | 4 | 2 | 2 | 2 |
| Resto | 2 | 296 | 1106 | 1486 |
En esta ocasión el escaño vale 1877 votos. Al final los escaños han quedado así:
A: 2+1+4 = 7
B: 1+1+2 = 4
C: 1+1+2 = 4
D: 2+1+2 = 5
Este reparto se aproxima más (en este caso coincide) al resultado buscado que el anterior, debido a que sólo usamos 2 precios distintos para el escaño en vez de X+1 lo que distorsiona menos la proporción (y eso que en el ejemplo X+1 es 3 tan sólo).
Este caso especial y mejorado de la "bolsa de restos" tampoco coincide necesariamente con un reparto equitativo. Vamos a ver un nuevo ejemplo sobre la bolsa de restos, para constatarlo. Tomaremos 3 partidos (A, B y C) y 2 distritos (J y K).
D’Hondt | A | B | C |
Votos | 20 | 5 | 10 |
Escaños | 1 | 0 | 0 |
Resto | 0 | 5 | 10 |
| D’Hondt | A | B | C |
| Votos | 2002 | 2002 | 1000 |
| Escaños | 2 | 2 | 0 |
| Resto | 0 | 0 | 1000 |
Hasta ahora A ha obtenido 3 escaños y B 2. En J el escaño vale 20 votos y en K vale 1001.
Veamos los que obtienen gracias a la bolsa de restos (suponemos que en el distrito global se reparten 5 escaños, tantos como la suma de los dos distritos):
| D’Hondt | A | B | C |
| Votos | 0 | 5 | 1010 |
| Escaños | 0 | 0 | 5 |
| Resto | 0 | 5 | 0 |
Veamos también el reparto de los restos asignando a los escaños un valor de 20 votos en J y K (caso mejorado de la bolsa de restos).
| D’Hondt | A | B | C |
| Votos | 1962 | 1967 | 1010 |
| Escaños | 2 | 2 | 1 |
| Resto | 0 | 5 | 29 |
Y por último, el reparto de 10 escaños en un sólo distrito (el caso equitativo en que cada escaño vale 501 votos):
| D’Hondt | A | B | C |
| Votos | 2022 | 2007 | 1010 |
| Escaños | 4 | 4 | 2 |
| Resto | 18 | 3 | 8 |
Comparemos los tres repartos:
| Escaños | A | B | C |
| Bolsa de restos | 3 | 2 | 5 |
| Bolsa mejorada | 5 | 4 | 1 |
| Reparto equitativo | 4 | 4 | 2 |
| Votos recibidos | 2022 | 2007 | 1010 |
Como puede observarse, ni con la mejora aplicada a la bolsa de restos (tomar 2 precios distintos del escaño en vez de X+1) se logra imitar el reparto equitativo, aunque resulta más desproporcionado aún el reparto con 3 precios distintos para el escaño. En la siguiente entrada seguiremos analizando sistemas electorales supuestamente equivalentes al reparto equitativo puro, que engañan a la intuición incluso más que el de la bolsa de restos.
Suscribirse a:
Entradas (Atom)